3 Mecanismes

 
Màquines y mecanismes

Fins ara ens hem ocupat de les màquines simples, la principal funció de les quals és multiplicar la força. Les màquines més complexes, a més de poder multiplicar o dividir forces, es caracteritzen per  transmetre i/o  transformar moviment. Aquestes màquines estan formades per diferents peces anomenades  mecanismes.

Un  mecanisme és un conjunt de peces (barres, politges, guies, etc.) que fan funcions de guiatge, transformació i transmissió del moviment relacionat amb les forces que actuen en una màquina.

Una bicicleta, una rentadora, una màquina de cosir; tots són exemples de màquines compostes per diferents mecanismes (pinyons, corretges, etc.).

En funció de si modifiquem o traslladem el moviment, parlem de  transmissió del moviment o  transformació del moviment.

SABIES QUE...

 3.1. Mecanismes de transmissió del moviment

Els mecanismes de transmissió del moviment permeten passar el moviment d’un eix a un altre, modificant la velocitat i el sentit de gir. Els més importants són: transmissió per  engranatges, per  cadenes i per  corretges.

Fig.2.37 Engranatges
Fig.2.38 Cadenes
Fig.2.39 Corretges
WEB

  INVESTIGA I EXPOSA!

Ens trobem a l’era digital, les noves tecnologies ens envolten: smartphones, tauletes tàctils, televisors d’alta definició, etc. I els rellotges? N’hi ha molts de digitals (electrònics), però també d’analògics (mecànics) amb unes prestacions excel·lents!

Fes una llista de dispositius o sistemes que utilitzin mecanismes per funcionar.

Exposa la qualitat d’aquests sistemes i valora si es podrien millorar.

 AVelocitat i relació de transmissió

Les politges, els engranatges i els pinyons són rodes que formen part dels mecanismes de transmissió del moviment circular. La velocitat a què giren s’anomena  freqüència de rotació (n) i s’expressa en voltes per minut o revolucions per minut (rpm).

La transmissió de moviment d’un eix a un altre es fa mitjançant rodes. En l’eix motriu o d’entrada hi tenim acoblada la  roda motriu, i a l’eix conduït o de sortida hi tenim la  roda conduïda.

La  relació de transmissió (i) indica el nombre de voltes que fa l’eix conduït (n2) per cada volta que fa l’eix motriu (n1) .

Matemàticament, la relació de transmissió s’expressa així:

\begin{equation*} i = \frac{n_{2}}{n_{1}} \end{equation*}

i = relació de transmissió (no té unitats)

n1 = freqüència de rotació de l’eix motriu o de la roda motriu (rpm)

n2 = freqüència de rotació de l’eix conduït o de la roda conduïda (rpm)


En funció del resultat de l’operació, podem tenir:

  1. i >1: la roda conduïda gira més ràpidament; per tant, és un sistema  multiplicador de velocitat.

  2. i <1: la roda conduïda gira més a poc a poc; per tant, és un sistema  reductor de velocitat.

En les transmissions de moviment, la  força transmesa és inversa a la velocitat. Així, en un sistema multiplicador de velocitat tenim un sistema reductor de força, i a l’inrevés.

Fig.2.40 . La maneta fa moure l’eix motriu solidari a la roda motriu (vermella). Aquesta transmet el moviment, mitjançant la cadena, a la roda conduïda (blava) i fa girar la busca que es troba solidària a l’eix conduït.
Fig.2.40 La maneta fa moure l’eix motriu solidari a la roda motriu (vermella). Aquesta transmet el moviment, mitjançant la cadena, a la roda conduïda (blava) i fa girar la busca que es troba solidària a l’eix conduït.
Fig.2.41 . Transmissió per engranatges
Fig.2.41 Transmissió per engranatges
Fig.2.42 . Transmissió per corretja
Fig.2.42 Transmissió per corretja
SABIES QUE...

En una transmissió per politges, la motriu gira a n1 = 300 rpm i la conduïda gira a n2 = 600 rpm . Calcula quina és la relació de transmissió. Es tracta d’un sistema reductor o multiplicador de velocitat?

Apliquem l’expressió de la relació de transmissió:

\begin{equation*} i = \frac{n_{2}}{n_{1}} = \frac{600\,rpm}{300\,rpm} = 2 \end{equation*}

Com que i = 2, llavors es tracta d’un sistema que  multiplica per dos la velocitat i  redueix per dos la força transmesa.

 
Tipus de corretges

La transmissió per corretges és una transmissió a distància mitjançant politges. Depenent de la velocitat i de la força que hàgim de transmetre, hem d’utilitzar un tipus de corretja o un altre.
Ara identificarem tipus de corretges.
Recorda que cada corretja té una utilitat determinada, les més utilitzades per garantir una bona transmissió i una velocitat elevada són les dentades.
dentada.jpg
planasfin.jpg
trapezoidal.jpg
especials.jpg
eslabon1.jpg
dentada
plana
trapezial
especials
de baules

  ACTIVITATS

16

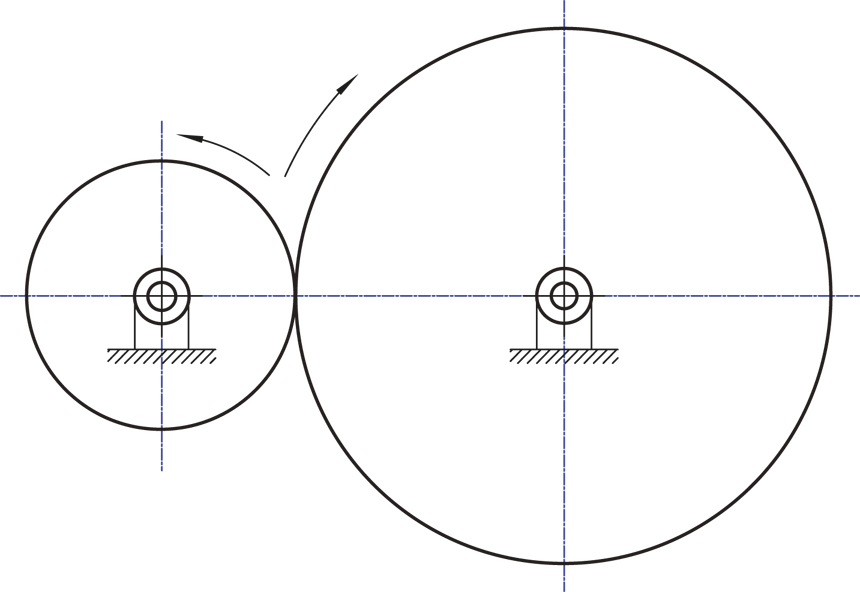
Identifica les parts d’aquesta transmissió.

 
Fig.2.43 .
Fig.2.43
17

Determina la freqüència de rotació de la roda motriu d’una transmissió per politges en què la roda conduïda gira a n2= 600 rpm i la relació de transmissió és de i = 3.

18

En l’activitat anterior, si la roda motriu girés a n1= 300 rpm, quina seria la relació de transmissió (i)?

 BTransmissió per corretges

Una de les aplicacions més importants de les politges és la transmissió d’un moviment giratori o de rotació d’un eix a un altre paral·lel. La  corretja és un sistema flexible i molt apropiat per dur a terme aquest tipus de transmissió. La corretja més usada és la de tipus  trapezial, però també s’usen les  planes i les  dentades.

Les  principals característiques són la facilitat i senzillesa per transmetre el moviment a llarga distància. No necessita un gran manteniment i és un sistema silenciós. Per contra, la corretja pot lliscar entre les politges i no és adequada per transmetre grans forces.

Fig.2.44 Transmissió per corretges planes i politges
Fig.2.45 Corretja dentada d’un motor d’automòbil
Fig.2.46 Corretges trapezials per a la transmissió de les politges d’un trepant de sobretaula

 
Càlcul de politges

La transmissió per politges permet transmetre moviments a llarga distància.
Si a partir d’una roda motriu volem obtenir diferents velocitats, podem tenir un sistema de politges. Amb les dades que es donen a continuació, calcula les diferents velocitats i la relació de transmissió del sistema de politges.
.
Roda 1 motriu: velocitat 1000 rpm D1 = 120mm
Roda 2: velocitat? D2 = 360 mm
Roda 3: velocitat? D3 = 150 mm
Roda 4: velocitat? D4 = 340 mm
Relació de transmissió?
Recorda que les politges que estan situades al mateix eix tenen la mateixa velocitat.
 Escribe aquí tu respuesta.
Velocitat rodes 2 i 3 és la mateixa
n2= n2 i n3 =333,33 rpm
Velocitat roda 4
n4= n4 = 147,05 rpm
Relació de transmissió i = 147,05/1000 = 0,147
Escriviuaquíl’equació.

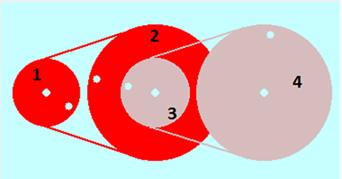
 Freqüències i relacions de transmissió de les politges

Si anomenem n1 i n2 les freqüències de rotació de la politja motriu i conduïda, respectivament, i D1 i D2 els seus  diàmetres, la relació de transmissió (i) la podem calcular fent servir l’expressió:

\begin{equation*} i = \frac{n_{2}}{n_{1}} = \frac{D_{1}}{D_{2}} \end{equation*}

En funció dels diàmetres i la disposició de les corretges, amb dues politges podem tenir quatre possibles acoblaments:

Fig.2.48 .
Fig.2.48

Per accionar un trepant de sobretaula (fig. 2.48) es col·loca una politja de 150 mm de diàmetre en un motor elèctric. Aquesta politja s’enllaça mitjançant una corretja amb una altra politja, que té un diàmetre de 100 mm, solidària a l’eix del trepant. Si el motor gira a 1500 rpm, quina serà la freqüència de rotació de l’eix conduït? Quina serà la relació de transmissió (i) del mecanisme?

Per determinar la freqüència de rotació, fem:

\begin{equation*} i = \frac{n_{2}}{n_{1}} = \frac{D_{1}}{D_{2}}\ ;\ n2 = \frac{n_{1} \cdot D_{1}}{D_{2}} = \frac{1\,500 \cdot 150}{100} = 2\,250\text{ rpm} \end{equation*}

Per determinar la relació de transmissió:

\begin{equation*} i = \frac{n_{2}}{n_{1}} = \frac{2\,250}{1\,500} = 1,5 \end{equation*}

Amb aquesta relació de transmissió, significa que per cada volta que fa el motor, el trepant en gira 1,5.

 
Càlcul d’engranatges

Quan fem els càlculs d’engranatges utilitzem la fórmula següent: n1·z1 = n2·z2. També podem calcular-ne la relació de transmissió.
A partir d’aquestes afirmacions cal revisar si els càlculs següents són correctes.
01)La relació de transmissió és 1,33.
04)La relació de transmissió és 0,5.
Si tenim un engranatge format per una roda motriu de 100 dents i la conduïda de 75 dents, la relació de transmissió és 1,5.
Si necessitem un engranatge amb una relació de transmissió de 0,25, format per una roda motriu de 50 dents, la roda conduïda ha de tenir 200 dents.
Si tenim un engranatge amb una roda conduïda de 50 dents i la relació de transmissió és 1, la roda motriu té 50 dents.
Si tenim una roda motriu amb una velocitat de 50 rad/s i una de conduïda de 25 rad/s, la relació de transmissió és 2.
Si un engranatge té una relació de transmissió 3 i la roda conduïda gira a 75 rad/s, la roda motriu gira a 25 rad/s.

 CTransmissió per engranatges

Els engranatges estan constituïts per  rodes dentades, de manera que les dents de l’una s’insereixen dins de l’altra. S’usen quan els eixos entre els quals s’ha de transmetre el moviment són molt propers. Els engranatges més comuns són: els  helicoïdals, els  rectes iels  cònics.

Fig.2.49 . Engranatges rectes en l’interior d’un rellotge
Fig.2.49 Engranatges rectes en l’interior d’un rellotge
Fig.2.50 . Helicoïdals
Fig.2.50 Helicoïdals
Fig.2.51 . Rectes
Fig.2.51 Rectes
Fig.2.52 . Cònics
Fig.2.52 Cònics

Les  principals característiques són: transmissió molt fiable i exacta, ja que no existeix el lliscament entre rodes. Poden transmetre esforços elevats. No són útils per a transmissions a distància.

SABIES QUE...

 Velocitats i relacions de transmissió dels engranatges

Si anomenem n1 i n2 les velocitats de rotació de l’engranatge motriu i conduït, respectivament, i z1 i z2, el seu  nombre de dents, la relació de transmissió (i) la podem calcular d’aquesta manera:

\begin{equation*} i = \frac{n_{2}}{n_{1}} = \frac{z_{1}}{z_{2}} \end{equation*}

En aquest tipus de transmissió, les dues rodes giren sincronitzades, però en sentit contrari. En funció del nombre de dents de les rodes, tenim  sistemes reductors o  multiplicadors de velocitat.

Fig.2.54 Sistemes de transmissió per engranatges
Fig.2.55 Per representar una transmissió per engranatges rectes, també es pot fer com a la figura, sense necessitat de dibuixar dents.
Fig.2.56 Transmissió per cadena entre plat i pinyons en una bicicleta
PER SABER-NE MÉS

  EXEMPLE 6

En una transmissió per engranatges, determina el nombre de dents que haurà de tenir l’engranatge motriu si s’acobla a un motor que gira a 800 rpm i l’engranatge conduït té 80 dents i ha de girar a 1 800 rpm. Determina també la relació de transmissió (i).

\begin{equation*} i = \frac{n_{2}}{n_{1}} = \frac{z_{1}}{z_{2}}\ ;\ z_{1} = \frac{n_{2} \cdot z_{2}}{n_{1}} = \frac{1\,800 \cdot 80}{800} = 180\textit{ dents} \end{equation*}
\begin{equation*} i = \frac{n_{2}}{n_{1}} = \frac{1\,800}{800} = 2,25 \end{equation*}

Per tant, es tracta d’un mecanisme multiplicador de velocitat.

 
Mecanismes biela-manovella i lleva

Tot just ara treballem els mecanismes de transformació de moviment, és a dir, passem de moviments circulars a rectilinis i a l’inrevés. Tot seguit analitzarem si han quedat clars els conceptes de funcionament d’aquests mecanismes.
02) La lleva només pot transformar un moviment circular en rectilini alternatiu.
03) És una transformació de moviment rectilini alternatiu en circular.
05) Tots dos mecanismes es poden trobar als motors de combustió interna.
La biela és un barra rígida que uneix la manovella i el pistó.
La lleva pot transformar un moviment circular en rectilini alternatiu i a l’inrevés.
Si en un mecanisme biela-manovella el pistó empeny la biela i aquesta fa girar la manovella, tenim un mecanisme que transforma un moviment circular en rectilini alternatiu.
La manovella pot fer un gir de 360º, però la biela no.
El mecanisme de biela-manovella el trobem als motors de combustió interna, però les lleves no.

 DTransmissió per cadenes

Aquest sistema incorpora els avantatges de les rodes dentades quant a la fiabilitat i la resistència de la transmissió, i el de les politges pel que fa a la distància entre eixos. Per contra, fa més soroll.

Fig.2.57

El càlcul de la velocitat i de les relacions de transmissió s’efectua com el dels engranatges, però les dues rodes, plat i pinyó, giren en el mateix sentit.

Fig.2.58 Transmissió per cadena en un una moto
PER SABER-NE MÉS
WEB

 
Càlculs

Un cop explicats tots els sistemes de transmissió de moviment, hem de saber com es calculen les velocitats de sortida i la relació de transmissió. Analitza matemàticament els mecanismes següents i selecciona la resposta correcta.
Recorda que el càlcul de politges es fa amb el diàmetre, i el d’engranatges i rodes dentades, per nombre de dents.
Tenim un motor que gira a 1000 rpm, unit a una roda dentada de 30 dents i una roda conduïda de 15. La transmissió es fa amb un mecanisme de transmissió per cadena. Quina és la velocitat de la roda conduïda?
Tenim un mecanisme format per dos tipus de transmissió. El primer és per engranatges, el motor està unit a l’engranatge de 100 dents i mou una roda de 50 dents. Al mateix eix de l’engranatge conduït hi ha una roda dentada de 10 dents que, mitjançant una transmissió per cadena, mou una altra roda de 40 dents. Calcula la velocitat de la roda de 40 dents (el motor gira a 1000 rpm).
Tenim un mecanisme format per dos tipus de transmissió. El primer és per corretges, el motor està unit a una politja de 20 mm de diàmetre i mou una politja de 40 mm. En el mateix eix de la politja conduïda hi ha una roda dentada de 20 dents que mitjançant una transmissió per cadena mou una altra roda de 40 dents. Calcula la velocitat de la roda de 40 dents (el motor gira a 1000 rpm).
Si tenim un tren d’engranatges format per 4 rodes, la primera de 20 dents, la segona de 10 dents, la tercera de 40 dents i la quarta de 60 dents, quina és la relació de transmissió total?
Tenim un mecanisme format per dos tipus de transmissió. El primer és per corretges, el motor està unit a una politja de 20 mm de diàmetre i en mou una altra de 40 mm. Al mateix eix de la politja conduïda hi ha una roda dentada de 15 dents que, mitjançant una transmissió per cadena, mou una altra roda de 30 dents. Calcula la relació de transmissió total.

 
Mecanismes

Has vist que hi ha molts mecanismes de transmissió de moviment. El que volem ara és relacionar una definició amb un sistema de transmissió.
Recorda que els mecanismes de transmissió més importants són per engranatges, per cadenes i per corretges.
Format per dues politges unides mitjançant un element flexible anomenat corretja
Format per dues rodes dentades unides per un element format per baules
Mecanisme utilitzat quan ens cal transmetre una velocitat elevada i que la corretja no llisqui
Format per rodes dentades, aquestes rodes actuen l’una sobre l’altra a través de dents que s’intercalen
Transmet moviment entre eixos que formen un angle recte i en un sol sentit
transmissió per corretja.
transmissió per cadena.
transmissió per corretja dentada.
engranatges.
cargol sense fi.

  ACTIVITATS

19

Elabora una taula en què s’indiquin els principals avantatges i inconvenients de la transmissió per politges, engranatges i cadenes.

20

En la transmissió per politges de la figura següent, la motriu té un diàmetre D1 = 100 mm i la conduïda D2 = 200 mm. Quina és la relació de transmissió? És un sistema reductor o multiplicador de la velocitat?

 
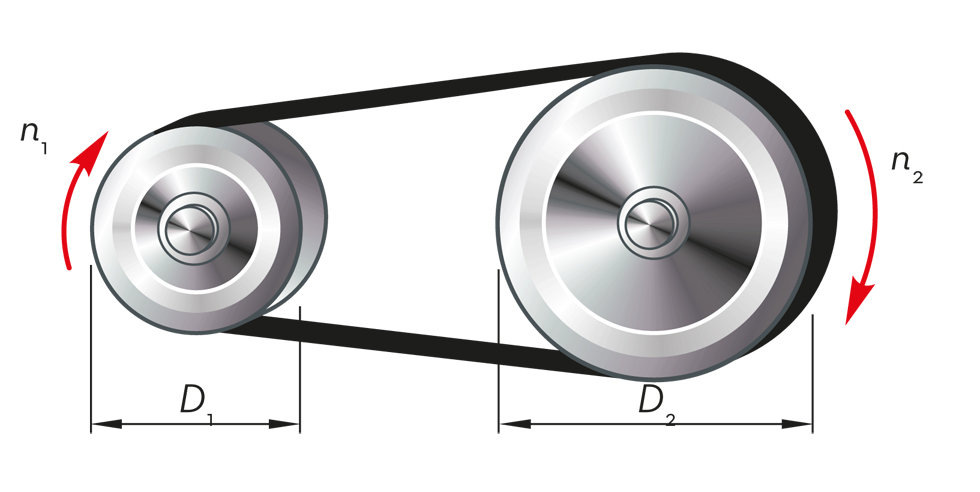Fig.2.59
21

Si sabem que la roda conduïda de l’exercici anterior gira a n2 = 1500 rpm, a quina freqüència gira la roda motriu?

22

Calcula la freqüència de rotació de l’engranatge 1 i la relació de transmissió d’aquest mecanisme, si la freqüència de rotació de l’engranatge 2 és de 250 rpm. Es tracta d’un sistema reductor o multiplicador de velocitat?

 
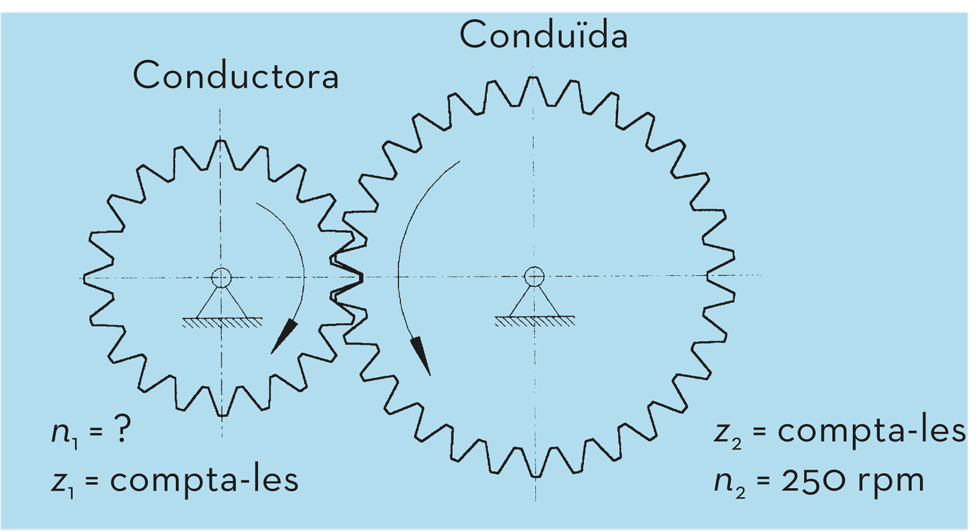Fig.2.60
23

Assenyala cap on es desplaçaran les cremalleres si l’engranatge número 1 es mou com s’indica a la fig. 2.61.
 
Fig.2.61

 3.2. Mecanismes de transformació del moviment

Els mecanismes que hem descrit fins ara transmeten moviments circulars. Els que estudiarem a continuació transformen el moviment circular en rectilini alternatiu o a l’inrevés. És el cas del mecanisme  biela-manovella i les  lleves.

Fig.2.62 Quatre mecanismes biela-manovella treballant en el cigonyal d’un motor de combustió interna d’un vehicle

 AMecanisme biela-manovella

El mecanisme biela-manovella transforma de manera il·limitada el  moviment circular en rectilini alternatiu i viceversa.

La  manovella o  maneta, anomenada també  cigonyal, duu acoblada, mitjançant una articulació, la  biela. En l’altre extrem de la biela es fixa una altra peça, anomenada  pistó. En girar la maneta fem que el pistó, a través de la biela, llisqui dins una guia de dreta a esquerra alternativament. Si fem moure el pistó alternativament aconseguirem fer girar la manovella.

La principal aplicació la trobem en els motors d’explosió (cotxes, motos, etc.). També és molt usat en les màquines de cosir.

SABIES QUE...

 BLleva

Les lleves s’utilitzen bàsicament per transformar moviments circulars en rectilinis alternatius, però no a l’inrevés, com passa amb el mecanisme biela-manovella.

Fig.2.65 Arbre de lleves d’un motor d’explosió
Fig.2.66 Mecanisme de lleva en l’obertura de les vàlvules d’un motor d’explosió

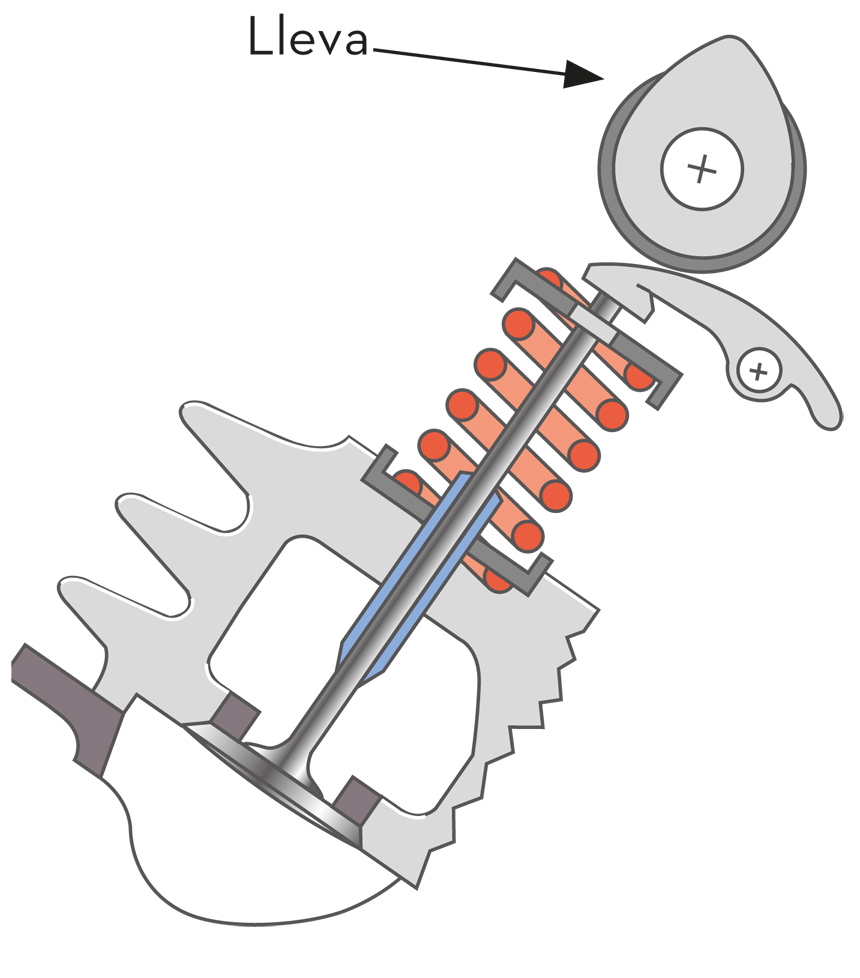
La principal aplicació és la que s’utilitza en els motors d’explosió per  obrir i tancar les vàlvules d’entrada i sortida de gasos del cilindre.

VÍDEO

 
Mecanismes biela-manovella i lleva

Tot just ara treballem els mecanismes de transformació de moviment, és a dir, passem de moviments circulars a rectilinis i a l’inrevés. Tot seguit analitzarem si han quedat clars els conceptes de funcionament d’aquests mecanismes.
02) La lleva només pot transformar un moviment circular en rectilini alternatiu.
03) És una transformació de moviment rectilini alternatiu en circular.
05) Tots dos mecanismes es poden trobar als motors de combustió interna.
La biela és un barra rígida que uneix la manovella i el pistó.
La lleva pot transformar un moviment circular en rectilini alternatiu i a l’inrevés.
Si en un mecanisme biela-manovella el pistó empeny la biela i aquesta fa girar la manovella, tenim un mecanisme que transforma un moviment circular en rectilini alternatiu.
La manovella pot fer un gir de 360º, però la biela no.
El mecanisme de biela-manovella el trobem als motors de combustió interna, però les lleves no.